L’objectif de toute étude et de tout test statistique est de démontrer de manière fiable des effets réels, parfois peu évidents au premier abord. Cependant, ce n’est souvent qu’en regardant dans les coulisses que l’on peut interpréter correctement les résultats statistiques. Il ne faut pas négliger, par exemple, la puissance statistique comme mesure de la pertinence des résultats, en particulier des résultats négatifs.
La qualité d’une étude ou d’un test dépend de nombreux facteurs – et est extrêmement pertinente pour l’interprétation des résultats. En effet, à quoi sert le traitement de données le plus sophistiqué si les résultats et les conclusions ont de fortes chances d’être erronés ? Une mesure de la puissance d’un test ou d’un plan d’étude est la puissance statistique, également connue sous le nom de pouvoir discriminant. Il n’est donc pas étonnant que les analyses correspondantes soient demandées par un nombre croissant de revues, de prestataires et de reviewers. En gros, le pouvoir discriminant décrit la probabilité qu’un effet soit détecté s’il existe réellement. En comparant le poids des souris et des éléphants, un test à puissance statistique élevée aurait donc plus de chances de donner des résultats indiquant un poids plus élevé des éléphants qu’un test à puissance statistique faible. Dans ce cas, l’hypothèse nulle serait : “Les souris sont aussi lourdes ou plus lourdes que les éléphants”. Cette hypothèse nulle (fausse) serait correctement rejetée par un test à pouvoir discriminant élevé, mais ne pourrait pas être réfutée par un test à pouvoir discriminant insuffisant. En d’autres termes, Avec une puissance statistique élevée, la probabilité de commettre une erreur de type II diminue. Mais ralentissons.
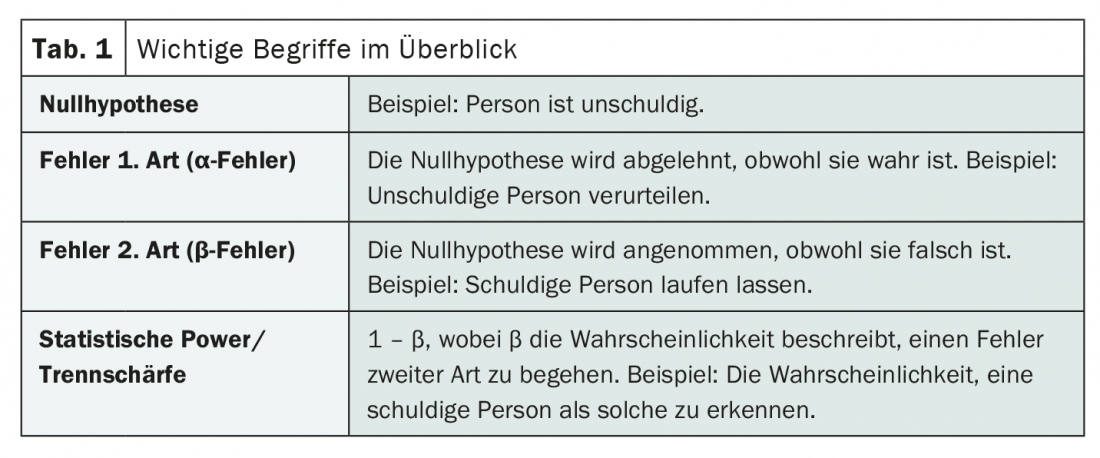
Des erreurs de premier et de second type
Alors que dans une erreur de premier type (également appelée erreur α), une hypothèse nulle correcte est rejetée, dans une erreur de second type (également appelée erreur β), une hypothèse nulle incorrecte est acceptée. Il n’est pas surprenant que cela soit rapidement oublié et souvent source de confusion. Un moyen mnémotechnique peut aider à résoudre ce problème : Si l’on part du principe qu’une personne est innocente (hypothèse zéro), la condamner malgré son innocence serait une erreur de premier type. Si l’on laisse cette personne en liberté et qu’elle est coupable, on commet une erreur de deuxième type.
La probabilité d’éviter une telle erreur de second type – c’est-à-dire l’acceptation erronée de l’hypothèse nulle – décrit maintenant le pouvoir discriminant ou la puissance statistique d’un test. Mathématiquement, celle-ci peut s’exprimer en conséquence par 1 – β si β est la probabilité de commettre une erreur de second type. Si β est petit, la puissance statistique est élevée. Et vice versa.
Puissance statistique : qu’est-ce qui est pris en compte ?
Outre la méthode statistique utilisée, d’autres facteurs déterminent la puissance statistique. Par exemple, il semble logique qu’une grande différence entre deux populations passe plus rarement inaperçue qu’une petite (il est plus facile de détecter la différence de poids entre des souris et des éléphants qu’entre des souris et des rats). Par conséquent, plus la différence réelle augmente, plus le pouvoir séparateur augmente. Il en va de même pour une dispersion de plus en plus faible. Plus la dispersion des données est faible, plus il est facile d’identifier les différences existantes. Ou encore : s’il y avait des souris de 5 tonnes et des éléphants de 20 grammes, la différence de poids serait sans doute moins facile à prouver. Un facteur important – et influençable – dans ce domaine est la taille de l’échantillon, car l’erreur standard diminue lorsque la taille de l’échantillon augmente. Ainsi, une taille d’échantillon plus importante permet de séparer plus facilement les petits effets. Le niveau de signification – c’est-à-dire la probabilité de commettre une erreur de premier type – est également pris en compte dans la puissance statistique.
Dans ce cadre, il est tout à fait pertinent d’évaluer le pouvoir discriminant d’un plan d’étude avant de le mettre en œuvre. En effet, à ce stade, la taille de l’échantillon, par exemple, peut encore être ajustée. Les analyses de puissance permettent de décider du nombre de sujets nécessaires pour mener une étude de manière pertinente. Une analyse de puissance effectuée a posteriori – généralement en l’absence de résultats significatifs – peut certes permettre de savoir combien de sujets supplémentaires auraient été nécessaires, mais elle est généralement trop tardive. Habituellement, on choisit un pouvoir discriminant d’environ 80%, la probabilité de manquer une différence significative est donc souvent de 20%. Une solution de compromis classique, après tout, une augmentation de la puissance statistique à 90% nécessiterait une augmentation d’environ 30% de la taille de l’échantillon. La conclusion est qu’un résultat d’étude négatif n’est pas nécessairement dû à une absence d’effet. Peut-être l’échantillon était-il trop petit, la dispersion trop importante, l’effet trop faible ou l’analyse statistique mal choisie.
Littérature :
- StatistikGuru, version 1.96 : puissance statistique. https://statistikguru.de/lexikon/statistische-power.html (dernier accès le 27.09.2021).
- Bortz J : Statistiques – pour les chercheurs en sciences sociales. 5e édition : Springer-Verlag Berlin Heidelberg ; 1999.
InFo ONKOLOGIE & HÉMATOLOGIE 2021 ; 9(5) : 25