Chaque jour, les spécialistes de l’oncologie sont littéralement inondés de nouvelles données et de résultats d’études. Et l’une d’entre elles est omniprésente : la valeur p. Se soustraire à son emprise tout en se tenant au courant relève de l’impossible. Après tout, c’est lui qui décide, par exemple, si un nouveau médicament est considéré comme efficace ou non. Mais que dit exactement la valeur p ?
La première chose à savoir : plus c’est petit, mieux c’est. Dans ce cas, c’est généralement vrai et la plupart des gens le savent, même si leurs études de statistiques remontent à quelques années et que leur intérêt est limité. Néanmoins, cette simplification grossière fait du tort à la valeur p, car il y a beaucoup plus derrière. Beaucoup plus, qui n’est pas si difficile à comprendre.
Sens et objectif
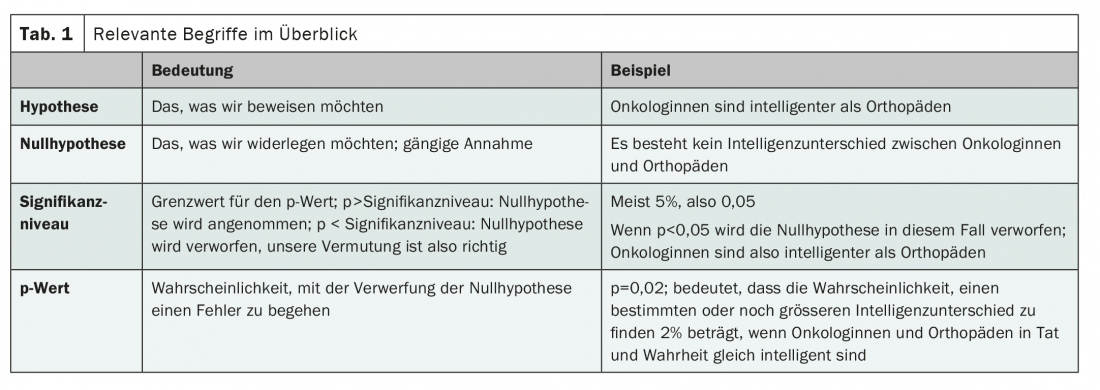
La valeur p a exactement une fonction. Il sert uniquement à maintenir ou à rejeter l’hypothèse nulle. Un exemple : la valeur p détermine si nous acceptons l’hypothèse selon laquelle les oncologues sont plus intelligents que les orthopédistes. Dans ce cas, notre hypothèse nulle serait “les oncologues sont aussi intelligents que les orthopédistes”. Si la valeur p calculée est inférieure au niveau de signification défini au préalable, nous pouvons supposer que notre hypothèse nulle est fausse, c’est-à-dire que les oncologues sont – conformément à nos attentes – plus intelligents que les orthopédistes. En revanche, si la valeur p est supérieure au niveau de signification, nous devons maintenir l’hypothèse nulle, la différence d’intelligence supposée n’est pas statistiquement significative.
Et quel est le niveau de signification ?
Le niveau de signification est fixé par les auteurs de l’étude eux-mêmes, dans la plupart des cas à 5%. C’est ainsi que l’on obtient la fameuse image p<0,05, que nous connaissons bien grâce à diverses publications – et qui correspond souvent à ce que nous voulons voir. En effet, p<0,05 signifie que l’hypothèse nulle peut être rejetée au niveau de signification fixé à 5%, c’est-à-dire que les oncologues sont plus intelligents que les orthopédistes. Le niveau de signification choisi représente une valeur limite. Il décrit la probabilité tolérée de faire une erreur en rejetant l’hypothèse nulle. Avec un niveau de signification de 5%, nous supposons dans notre exemple, pour accepter notre supposition (que les oncologues sont plus intelligents que les orthopédistes), que le risque de faire une fausse déclaration à ce sujet doit être inférieur à 5%. Si nous réduisons la valeur critique à 1%, la probabilité d’erreur est plus faible, mais il est également plus difficile de confirmer notre hypothèse. Inversement, nous pouvons augmenter le niveau de signification à 50% – avec pour conséquence que notre affirmation a une probabilité de 50% d’être fausse et donc sans pertinence.
Grâce à la compréhension du niveau de signification, il est maintenant facile de comprendre la signification de la valeur p. En effet, celui-ci indique le risque de faire une erreur en rejetant l’hypothèse nulle. Il s’agit donc d’une mesure de la probabilité du résultat, ou de résultats encore plus extrêmes, si l’hypothèse nulle est vraie. Ainsi, si notre étude conclut que les oncologues ont en moyenne 20 points de QI de plus que les orthopédistes, la valeur p est une mesure de la probabilité d’observer une différence de QI de 20 points de QI ou plus dans notre échantillon, alors qu’en réalité, il n’y a pas de différence de QI. Si la valeur p est de 0,01, la probabilité de faire une telle erreur est de 1%. Dans ce cas, s’il n’y a pas de différence de QI dans la population, il n’y a que 1% de chances de tirer un échantillon avec un écart de 20 points de QI ou plus. Tout est clair ?
Source : Fahrmeir L, et al. : Statistiques : la voie vers l’analyse des données. 8e édition. Springer Spektrum ; 2016.
InFo ONKOLOGIE & HÉMATOLOGIE 2021 ; 9(3) : 26
InFo PNEUMOLOGIE & ALLERGOLOGIE 2021 ; 3(4) : 27