Dans de nombreuses études cliniques, l’analyse de régression constitue une base importante de l’évaluation statistique – et donc des résultats trouvés. Par exemple, la plupart des médecins ont sans doute déjà entendu parler de la régression de Cox. Il est possible de démontrer mathématiquement si les variables A et B présentent une relation linéaire depuis le développement de la régression par Galton à la fin du 19e siècle. Jusqu’à aujourd’hui, beaucoup de choses ont été faites pour pouvoir représenter des interactions complexes.
Souvent, la problématique d’un essai clinique est claire : x est-il lié à y ? Ou, pour prendre un exemple plus concret et largement utilisé en oncologie : L’âge du patient a-t-il un impact sur la survie globale ? Dans ce cas, l’âge peut être désigné comme variable indépendante et la survie globale comme variable dépendante. Nous étudions donc les effets potentiels de la variable indépendante sur la variable dépendante. Jusqu’ici, c’est simple. L’influence d’autres facteurs – d’autres variables indépendantes – vient à chaque fois compliquer la situation. Ainsi, l’âge n’est pas le seul facteur à influencer les résultats, mais aussi, par exemple, le traitement, le sexe et peut-être même la phase lunaire pendant l’administration du médicament. Ce qui nous amène à un point important à ne jamais oublier dans l’interprétation des analyses de régression : comme chacun sait, une corrélation n’implique pas une causalité !
Idéalement, une analyse de régression devrait pouvoir distinguer les différents effets de différentes variables indépendantes sur la variable dépendante. Il existe aujourd’hui un grand nombre de méthodes statistiques qui peuvent être utilisées en fonction de la situation et des questions posées. Il est également important de faire la distinction entre l’analyse de régression et l’analyse de variance.
Différentes formes d’analyse de régression
Le choix de la méthode d’analyse la plus appropriée dépend du nombre de variables à étudier et du type d’échelle (tableau 1) [2]. En principe, pour une analyse de régression linéaire, il doit y avoir une relation linéaire entre les variables. Le coefficient de corrélation de Pearson est une mesure de la linéarité entre deux variables . En outre, les variables indépendantes ne doivent pas être corrélées entre elles et doivent être distribuées selon une loi à peu près normale [2]. Une autre condition est l’homoscédasticité : la valeur d’erreur de la variable indépendante doit être la même pour chaque valeur. Le logiciel statistique fait ensuite le reste, le “coefficient de détermination”R2 exprimant la mesure dans laquelle l’équation de régression reflète bien la relation entre les variables. Le test F et, dans le cas de plusieurs variables indépendantes, le test t [3] déterminent si la corrélation trouvée est statistiquement significative – et peut donc être transférée de l’échantillon à la population.
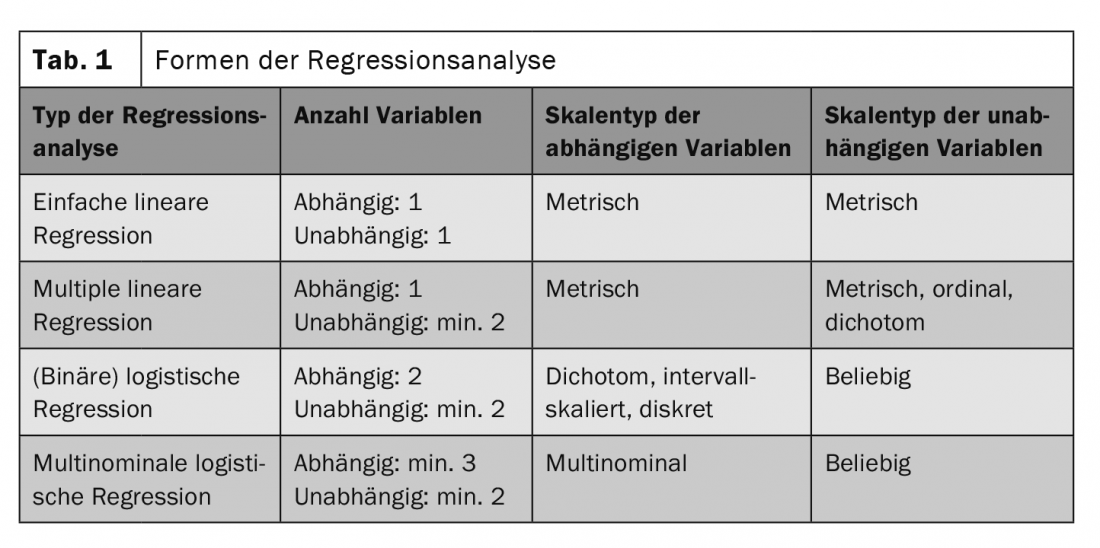
d’après [2]
Et quelle est la différence entre et l’analyse de variance (ANOVA) ?
L’analyse de régression et l’analyse de variance( ANOVA) sont toutes deux des méthodes standard dans divers programmes statistiques et leurs domaines d’application se recoupent. Alors que l’analyse de régression a été développée à l’origine pour étudier des variables métriques indépendantes telles que l’âge, l’analyse de variance a surtout servi, à l’origine, à analyser des variables indépendantes nominales telles que le choix du traitement. Les deux méthodes d’analyse peuvent aujourd’hui être utilisées avec des variables indépendantes métriques ou nominales [4]. Le bon choix n’est donc pas si simple, il s’agit généralement d’une question légitime qui doit être discutée avec un statisticien.
Littérature :
- Hemmerich W : StatistikGuru Version 1.96 : Régression, analyse de régression. https://statistikguru.de/lexikon/regression-regressionsanalyse.html (dernier accès le 23.12.2021)
- Qualtrics : Analyse de régression : processus, objectifs & exemples. www.qualtrics.com/de/erlebnismanagement/marktforschung/regressionsanalyse (dernier accès le 23.12.2021)
- Analyse de régression – Statista Definition https://de.statista.com/statistik/lexikon/definition/113/regressionsanalyse/ (dernier accès le 23/12/2021)
- Smigierski J : Quand faut-il calculer une analyse de variance et quand faut-il calculer une analyse de régression ? www.beratung-statistik.de/statistik-infos/statistik-beratung-faqs/unterschied-varianzanalyse-regressionsanalyse (dernier accès le 23.12.2021)
DERMATOLOGIE PRATIQUE 2022 ; 32(1) : 48
InFo ONKOLOGIE & HÉMATOLOGIE 2022 ; 10(1) : 41