Em muitos estudos clínicos, a análise de regressão é uma base importante de avaliação estatística – e, portanto, dos resultados encontrados. Por exemplo, a maioria dos médicos terá ouvido ou lido sobre a regressão de Cox. Se as variáveis A e B têm uma relação linear pode ser provada matematicamente desde o desenvolvimento da regressão no final do século XIX por Galton. Até hoje, muito tem sido feito para se poder mapear mesmo interacções complexas.
Muitas vezes a questão de um ensaio clínico é clara: está x relacionado com y? Ou, para dar um exemplo mais concreto que é amplamente utilizado em oncologia: A idade do paciente tem algum efeito na sobrevivência global? Neste caso, a idade pode ser chamada a variável independente e a sobrevivência global a variável dependente. Assim, examinamos os efeitos potenciais da variável independente sobre a variável dependente. Até agora, tão simples. A influência de outros factores – outras variáveis independentes – é um factor de complicação adicional em cada caso. Assim, não só a idade influencia o resultado, mas também, por exemplo, a terapia, o sexo e talvez mesmo a fase da lua durante a administração de medicamentos. O que nos leva a um ponto importante que nunca deve ser esquecido na interpretação das análises de regressão: Como é bem sabido, uma correlação não implica causalidade!
Idealmente, uma análise de regressão deveria ser capaz de distinguir os diferentes efeitos das diferentes variáveis independentes sobre a variável dependente. Actualmente, existe uma multiplicidade de métodos estatísticos para este fim, que são utilizados em função da situação e da questão. É também importante distinguir entre a regressão e a análise de variância.
Diferentes formas de análise de regressão
A escolha do método de análise mais apropriado depende do número de variáveis a estudar e do tipo de escala (Quadro 1) [2]. Em princípio, para uma análise de regressão linear, deve haver uma relação linear entre as variáveis. Uma medida de linearidade entre duas variáveis é o coeficiente de correlação de Pearson . Além disso, as variáveis independentes não devem estar correlacionadas entre si e devem ser distribuídas aproximadamente normalmente [2]. Outro requisito é a homocedasticidade: o valor de erro da variável independente deve ser o mesmo para cada valor. O resto é então feito pelo software estatístico, em que o chamado “coeficiente de determinação”R2 expressa quão bem a equação de regressão reflecte a relação entre as variáveis. Se a correlação encontrada é estatisticamente significativa – e portanto pode ser transferida da amostra para a população – é determinada pelo teste F e, no caso de várias variáveis independentes, pelo teste t [3].
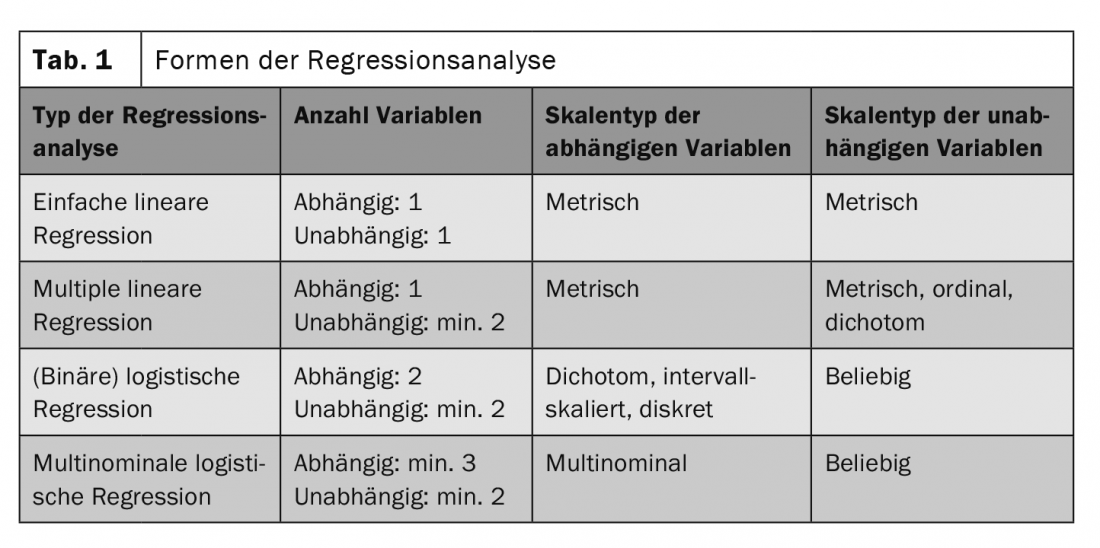
de acordo com [2]
E qual é a diferença entre e a análise de variância (ANOVA)?
A análise de regressão e a análise de variância( ANOVA) são ambos métodos padrão em vários programas estatísticos, e as áreas de aplicação sobrepõem-se. Enquanto a análise de regressão foi originalmente desenvolvida para examinar variáveis métricas independentes como a idade, a análise da variância na sua origem serviu principalmente para analisar variáveis nominais independentes como a escolha de tratamento. Ambos os métodos de análise podem ser utilizados hoje em dia com métrica, bem como com variáveis nominais independentes [4]. Portanto, a escolha certa não é assim tão fácil, na sua maioria uma questão legítima e deve ser discutida com um estatístico.
Literatura:
- Hemmerich W: StatistikGuru Versão 1.96: Regressão, Análise de Regressão. https://statistikguru.de/lexikon/regression-regressionsanalyse.html (último acesso 23.12.2021)
- Qualtrics: Análise de Regressão: Procedimento, Objectivos & Exemplos. www.qualtrics.com/de/erlebnismanagement/marktforschung/regressionsanalyse (último acesso 23.12.2021)
- Análise de regressão – definição estatística https://de.statista.com/statistik/lexikon/definition/113/regressionsanalyse/ (último acesso 23.12.2021)
- Smigierski J: Quando deve ser calculada uma análise de variância e quando uma análise de regressão? www.beratung-statistik.de/statistik-infos/statistik-beratung-faqs/unterschied-varianzanalyse-regressionsanalyse (último acesso 23.12.2021)
PRÁTICA DA DERMATOLOGIA 2022; 32(1): 48
InFo ONCOLOGy & HEMATOLOGy 2022; 10(1): 41