L’obiettivo di ogni studio e di ogni test statistico è quello di dimostrare in modo affidabile gli effetti che sono effettivamente presenti e che a volte non sono chiaramente evidenti a prima vista. Tuttavia, spesso solo uno sguardo dietro le quinte consente una corretta interpretazione dei risultati statistici. Ad esempio, la potenza statistica come misura della significatività dei risultati negativi, in particolare, non deve essere trascurata.
La qualità di uno studio o di un test dipende da molti fattori – ed è estremamente rilevante per l’interpretazione dei risultati. Dopotutto, a cosa serve l’elaborazione più elaborata dei dati se è molto probabile che i risultati e le conclusioni siano sbagliati? Una misura della significatività di un test o di un disegno di studio è la potenza statistica, nota anche come potere discriminatorio. Non c’è da stupirsi che le analisi corrispondenti siano richieste da un numero sempre maggiore di riviste, top performer e revisori. In parole povere, il potere discriminatorio descrive la probabilità di rilevare un effetto se effettivamente esiste. Quindi, quando si confronta il peso dei topi e degli elefanti, un test con un’elevata potenza statistica avrebbe maggiori probabilità di produrre risultati che suggeriscono un peso maggiore degli elefanti rispetto a un test con una bassa potenza statistica. In questo caso, l’ipotesi nulla sarebbe: “I topi hanno lo stesso peso o sono più pesanti degli elefanti”. Questa (falsa) ipotesi nulla verrebbe respinta correttamente da un test con un elevato potere discriminatorio, ma non potrebbe essere confutata da un test con un potere discriminatorio insufficiente. In altre parole: Con un’elevata potenza statistica, la probabilità di commettere un errore di Tipo II diminuisce. Ma rallenta.
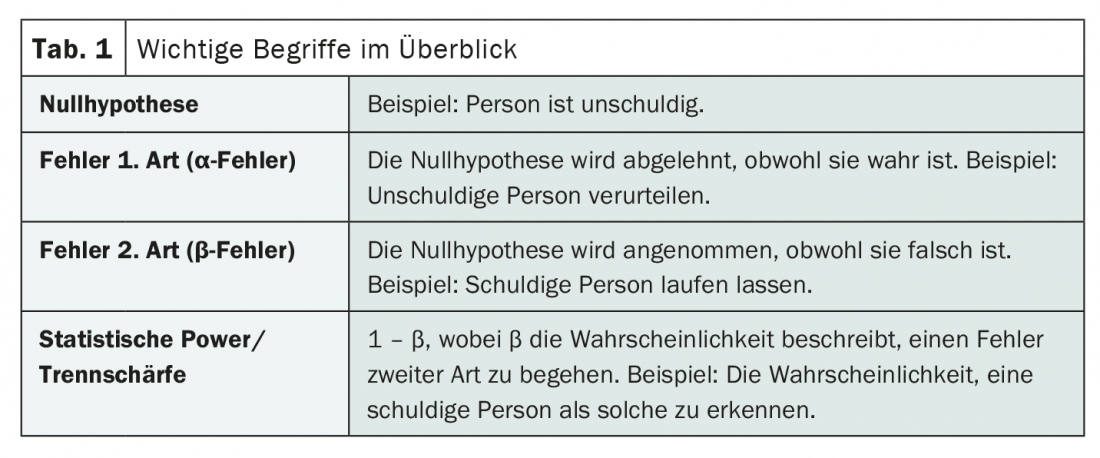
Di errori del primo e del secondo tipo
Mentre un’ipotesi nulla corretta viene rifiutata nel caso di un errore di primo tipo (anche α-errore), un’ipotesi nulla falsa viene accettata nel caso di un errore di secondo tipo (anche β-errore). Non sorprende che questo venga dimenticato rapidamente e che spesso generi confusione. Un mnemonico può essere d’aiuto in questo caso: Se si presume l’innocenza di una persona (ipotesi nulla), la condanna nonostante l’innocenza sarebbe un errore del primo tipo. Se la persona in questione venisse lasciata andare e fosse colpevole, invece, si commetterebbe un errore del secondo tipo.
La probabilità di evitare questo secondo tipo di errore – cioè l’accettazione errata dell’ipotesi nulla – descrive il potere discriminatorio o il potere statistico di un test. Matematicamente, questo può essere espresso in conseguenza come 1 – β, quando β è la probabilità di commettere un secondo tipo di errore. Se β è piccolo, la potenza statistica è elevata. E viceversa.
Potere statistico: cosa entra?
Oltre al metodo statistico utilizzato, altri fattori determinano la potenza statistica. Per esempio, sembra logico che una grande differenza tra due popolazioni abbia meno probabilità di essere trascurata rispetto a una piccola (è più facile rilevare la differenza di peso tra topi ed elefanti che quella tra topi e ratti). Quindi, con una differenza effettiva crescente, aumenta anche il potere discriminatorio. Lo stesso vale per una dispersione decrescente. Più piccola è la dispersione dei dati, meglio si possono riconoscere le differenze. Oppure: se ci fossero topi che pesano 5 tonnellate ed elefanti che pesano 20 grammi, la differenza di peso sarebbe probabilmente meno facile da dimostrare. Un fattore importante – e influenzabile – in quest’area è la dimensione del campione, poiché l’errore standard diventa più piccolo con l’aumento della dimensione del campione. Quindi, è più probabile che gli effetti più piccoli siano separati da un campione di dimensioni maggiori. Il livello di significatività – cioè la probabilità di commettere un errore del primo tipo – confluisce anche nella potenza statistica.
In questo quadro, ha senso valutare il potere discriminatorio di un disegno di studio prima che venga implementato. Perché a questo punto, ad esempio, la dimensione del campione può ancora essere modificata. Le analisi di potenza possono essere utilizzate per decidere quanti soggetti sono necessari per condurre uno studio in modo significativo. Un’analisi di potenza effettuata successivamente – di solito in assenza di risultati significativi – può fornire informazioni su quanti soggetti aggiuntivi sarebbero stati necessari, ma di solito è troppo tardi. Di solito si sceglie un potere discriminatorio intorno all’80%, quindi la probabilità di perdere una differenza significativa è spesso intorno al 20%. Una classica soluzione di compromesso, dopo tutto, un aumento della potenza statistica al 90% richiederebbe un aumento del 30% circa della dimensione del campione. La conclusione: un risultato negativo di uno studio non è necessariamente dovuto a una mancanza di effetto. Forse il campione era troppo piccolo, la dispersione troppo grande, l’effetto troppo debole o la valutazione statistica mal scelta.
Letteratura:
- StatistikGuru, versione 1.96: Potenza statistica. https://statistikguru.de/lexikon/statistische-power.html (ultimo accesso 27.09.2021).
- Bortz J: Statistica – per gli scienziati sociali. 5a edizione: Springer-Verlag Berlin Heidelberg; 1999.
InFo ONCOLOGIA ED EMATOLOGIA 2021; 9(5): 25