O objectivo de cada estudo e de cada teste estatístico é demonstrar de forma fiável os efeitos que estão realmente presentes e por vezes não claramente aparentes à primeira vista. No entanto, muitas vezes apenas um olhar nos bastidores permite uma interpretação correcta dos resultados estatísticos. Por exemplo, o poder estatístico como medida do significado de resultados negativos em particular não deve ser desconsiderado.
A qualidade de um estudo ou de um teste depende de muitos factores – e é extremamente relevante para a interpretação dos resultados. Afinal, qual é a utilidade do processamento de dados mais elaborado se os resultados e conclusões são muito susceptíveis de estarem errados? Uma medida do significado de uma concepção de teste ou estudo é o poder estatístico, também conhecido como poder discriminatório. Não admira que as análises correspondentes sejam exigidas por cada vez mais revistas, top performers e revisores. Grosseiramente falando, o poder discriminatório descreve a probabilidade de detectar um efeito se este existir realmente. Assim, ao comparar o peso de ratos e elefantes, um teste com elevado poder estatístico teria mais probabilidades de produzir resultados sugerindo um maior peso de elefantes do que um teste com baixo poder estatístico. Neste caso, a hipótese nula seria: “Os ratos têm o mesmo peso ou são mais pesados que os elefantes”. Esta hipótese (falsa) nula seria correctamente rejeitada por um teste com elevado poder discriminatório, mas não poderia ser refutada por um teste com insuficiente poder discriminatório. Por outras palavras: Com um elevado poder estatístico, a probabilidade de cometer um erro de Tipo II diminui. Mas abrandar.
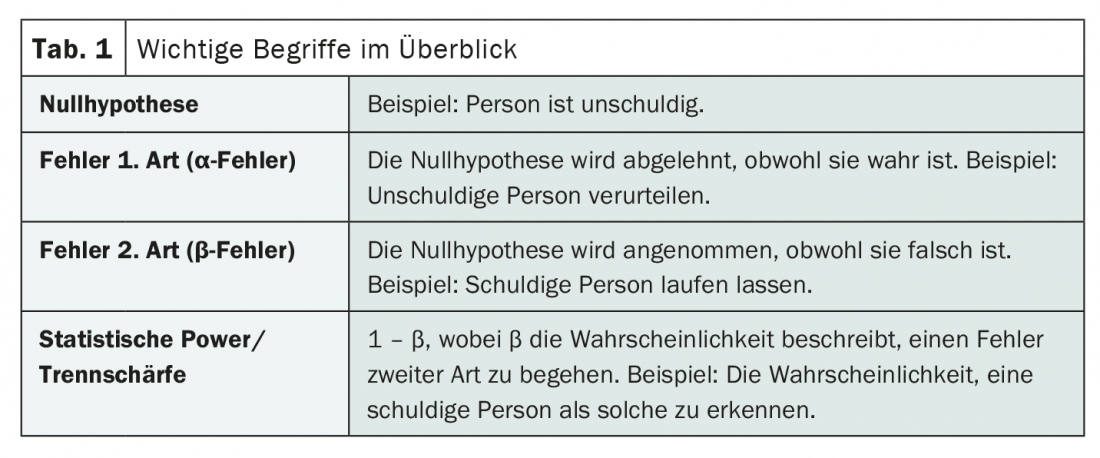
De erros de primeiro e segundo tipo
Enquanto uma hipótese nula correcta é rejeitada no caso de um primeiro tipo de erro (também α-error), uma hipótese nula falsa é aceite no caso de um segundo tipo de erro (também β-error). O facto de isto ser rapidamente esquecido e levar frequentemente à confusão não é surpreendente. Uma mnemónica pode ajudar aqui: Se se assume a inocência de uma pessoa (hipótese nula), a condenação apesar da inocência seria um erro do primeiro tipo. Se a pessoa em questão fosse libertada e fosse culpada, por outro lado, seria cometido um erro do segundo tipo.
A probabilidade com que esse segundo tipo de erro – ou seja, a aceitação errada da hipótese nula – pode ser evitada descreve agora o poder discriminatório ou o poder estatístico de um teste. Matematicamente, isto pode ser expresso em consequência como 1 – β, quando β é a probabilidade de cometer um segundo tipo de erro. Se β for pequeno, o poder estatístico é elevado. E vice versa.
Poder estatístico: Em que flui?
Para além do método estatístico utilizado, outros factores determinam o poder estatístico. Por exemplo, parece lógico que uma grande diferença entre duas populações é menos susceptível de ser negligenciada do que uma pequena (é mais fácil detectar a diferença de peso entre ratos e elefantes do que a diferença entre ratos e ratazanas). Assim, com uma diferença real crescente, o poder discriminatório também aumenta. O mesmo se aplica a uma dispersão decrescente. Quanto menor for a dispersão de dados, melhores serão as diferenças existentes que podem ser reconhecidas. Ou: Se houvesse ratos com 5 toneladas e elefantes com 20 gramas, a diferença de peso seria provavelmente menos fácil de provar. Um factor importante – e influenciável – nesta área é o tamanho da amostra, uma vez que o erro padrão se torna menor com o aumento do tamanho da amostra. Assim, os efeitos mais pequenos são mais susceptíveis de serem separados por uma amostra de maior dimensão. O nível de significância – ou seja, a probabilidade de cometer um erro do primeiro tipo – também flui para o poder estatístico.
Neste quadro, faz sentido avaliar o poder discriminatório de um desenho de estudo antes de este ser implementado. Porque nesta altura, por exemplo, o tamanho da amostra ainda pode ser ajustado. As análises de poder podem ser utilizadas para decidir quantos sujeitos são necessários para realizar um estudo de uma forma significativa. Uma análise de poder realizada posteriormente – geralmente na ausência de resultados significativos – pode fornecer informações sobre quantos assuntos adicionais teriam sido necessários, mas geralmente é demasiado tarde. Normalmente é escolhido um poder discriminatório de cerca de 80%, pelo que a probabilidade de faltar uma diferença significativa é muitas vezes de cerca de 20%. Uma solução de compromisso clássica, afinal, um aumento do poder estatístico para 90% exigiria um aumento de cerca de 30% no tamanho da amostra. A conclusão: Um resultado negativo do estudo não se deve necessariamente a uma falta de efeito. Talvez a amostra fosse demasiado pequena, a dispersão demasiado grande, o efeito demasiado fraco ou a avaliação estatística mal escolhida.
Literatura:
- StatistikGuru, Versão 1.96: Poder estatístico. https://statistikguru.de/lexikon/statistische-power.html (último acesso: 27.09.2021).
- Bortz J: Estatística – para cientistas sociais. 5ª edição: Springer-Verlag Berlin Heidelberg; 1999.
InFo ONCOLOGy & HEMATOLOGy 2021; 9(5): 25