In molti studi clinici, l’analisi di regressione è una base importante della valutazione statistica – e quindi dei risultati trovati. Ad esempio, la maggior parte dei medici avrà sentito parlare o letto della regressione di Cox. Se le variabili A e B hanno una relazione lineare può essere dimostrato matematicamente dallo sviluppo della regressione alla fine del XIX secolo da parte di Galton. Fino ad oggi, è stato fatto molto per poter mappare anche le interazioni complesse.
Spesso la domanda di uno studio clinico è chiara: x è correlato a y? Oppure, per fare un esempio più concreto, ampiamente utilizzato in oncologia: L’età del paziente ha un effetto sulla sopravvivenza globale? In questo caso, l’età può essere definita la variabile indipendente e la sopravvivenza globale la variabile dipendente. Quindi esaminiamo i potenziali effetti della variabile indipendente sulla variabile dipendente. Fin qui, tutto semplice. L’influenza di altri fattori – altre variabili indipendenti – è un ulteriore fattore di complicazione in ogni caso. Quindi, non solo l’età influenza l’esito, ma anche, ad esempio, la terapia, il sesso e forse anche la fase lunare durante la somministrazione dei farmaci. Il che ci porta a un punto importante che non dovrebbe mai essere dimenticato nell’interpretazione delle analisi di regressione: come è noto, una correlazione non implica la causalità!
Idealmente, un’analisi di regressione dovrebbe essere in grado di distinguere i diversi effetti delle diverse variabili indipendenti sulla variabile dipendente. Oggi esiste una moltitudine di metodi statistici per questo scopo, che vengono utilizzati a seconda della situazione e della domanda. È anche importante distinguere tra regressione e analisi della varianza.
Diverse forme di analisi di regressione
La scelta del metodo di analisi più appropriato dipende dal numero di variabili da studiare e dal tipo di scala (Tabella 1) [2]. In linea di principio, per un’analisi di regressione lineare, deve esistere una relazione lineare tra le variabili. Una misura della linearità tra due variabili è il coefficiente di correlazione di Pearson . Inoltre, le variabili indipendenti non devono essere correlate tra loro e devono avere una distribuzione approssimativamente normale [2]. Un altro requisito è l’omoscedasticità: il valore dell’errore della variabile indipendente deve essere lo stesso per ogni valore. Il resto lo fa il software statistico, dove il cosiddetto “coefficiente di determinazione”R2 esprime quanto l’equazione di regressione rifletta la relazione tra le variabili. Se la correlazione trovata è statisticamente significativa – e quindi può essere trasferita dal campione alla popolazione – è determinato dal test F e, nel caso di diverse variabili indipendenti, dal test t [3].
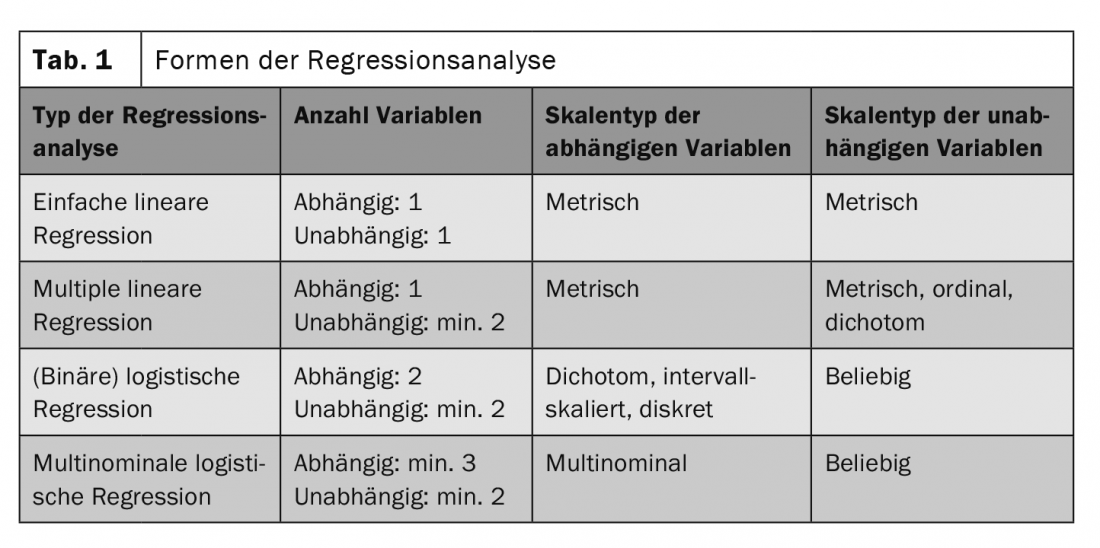
secondo [2]
E qual è la differenza tra e l’analisi della varianza (ANOVA)?
L’analisi di regressione e l’analisi della varianza( ANOVA) sono entrambi metodi standard in vari programmi statistici e le aree di applicazione si sovrappongono. Mentre l’analisi di regressione è stata originariamente sviluppata per esaminare le variabili metriche indipendenti, come l’età, l’analisi della varianza nella sua origine è servita principalmente per analizzare le variabili indipendenti nominali, come la scelta del trattamento. Entrambi i metodi di analisi possono essere utilizzati oggi con variabili indipendenti metriche e nominali [4]. Quindi la scelta giusta non è così facile, ma è una domanda legittima e dovrebbe essere discussa con uno statistico.
Letteratura:
- Hemmerich W: StatistikGuru Versione 1.96: Regressione, Analisi di regressione. https://statistikguru.de/lexikon/regression-regressionsanalyse.html (ultimo accesso 23.12.2021)
- Qualtrics: Analisi di regressione: procedura, obiettivi ed esempi. www.qualtrics.com/de/erlebnismanagement/marktforschung/regressionsanalyse (ultimo accesso 23.12.2021)
- Analisi di regressione – Definizione Statista https://de.statista.com/statistik/lexikon/definition/113/regressionsanalyse/ (ultimo accesso 23.12.2021)
- Smigierski J: Quando deve essere calcolata un’analisi della varianza e quando un’analisi di regressione? www.beratung-statistik.de/statistik-infos/statistik-beratung-faqs/unterschied-varianzanalyse-regressionsanalyse (ultimo accesso 23.12.2021)
PRATICA DERMATOLOGICA 2022; 32(1): 48
InFo ONCOLOGIA & EMATOLOGIA 2022; 10(1): 41