El objetivo de todo estudio y de toda prueba estadística es demostrar de forma fiable unos efectos que están realmente presentes y que a veces no se aprecian claramente a primera vista. Sin embargo, a menudo sólo una mirada entre bastidores permite interpretar correctamente los resultados estadísticos. Por ejemplo, no debe despreciarse la potencia estadística como medida de la importancia de los resultados negativos en particular.
La calidad de un estudio o de una prueba depende de muchos factores, y es muy relevante para la interpretación de los resultados. Al fin y al cabo, ¿de qué sirve el tratamiento de datos más elaborado si es muy probable que los resultados y las conclusiones sean erróneos? Una medida de la importancia de una prueba o del diseño de un estudio es la potencia estadística, también conocida como potencia discriminatoria. No es de extrañar que los análisis correspondientes sean exigidos cada vez por más revistas, altos cargos y revisores. A grandes rasgos, el poder discriminatorio describe la probabilidad de detectar un efecto si realmente existe. Así, al comparar el peso de ratones y elefantes, una prueba con una potencia estadística elevada tendría más probabilidades de producir resultados que sugirieran un mayor peso de los elefantes que una prueba con una potencia estadística baja. En este caso, la hipótesis nula sería: “Los ratones pesan lo mismo o más que los elefantes”. Esta hipótesis nula (falsa) sería rechazada correctamente por una prueba con un alto poder discriminatorio, pero no podría ser refutada por una prueba con un poder discriminatorio insuficiente. En otras palabras: Con una potencia estadística elevada, la probabilidad de cometer un error de tipo II disminuye. Pero más despacio.
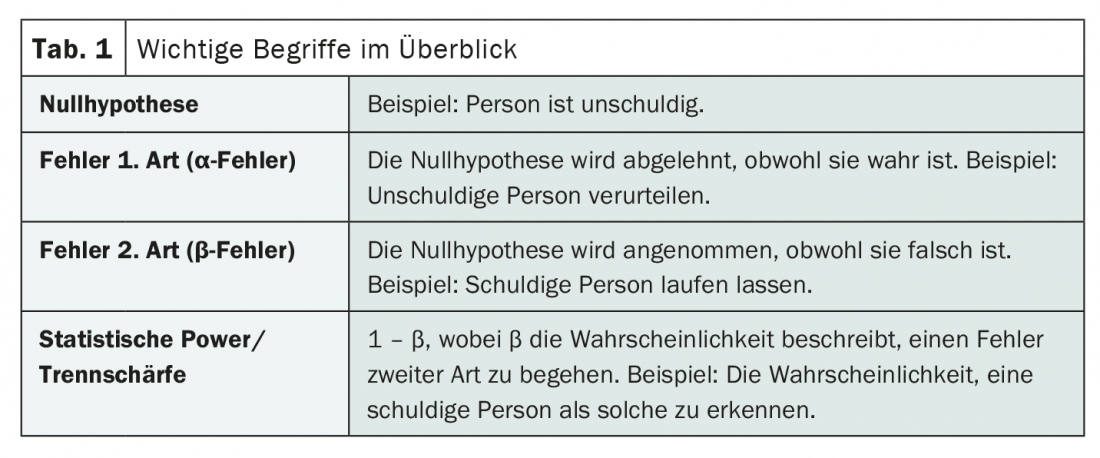
De errores de primer y segundo tipo
Mientras que en el caso de un error de primer tipo (también α-error) se rechaza una hipótesis nula correcta, en el caso de un error de segundo tipo (también β-error) se asume una hipótesis nula falsa. Que esto se olvide rápidamente y a menudo lleve a confusión no es sorprendente. Una mnemotecnia puede ayudar en este caso: Si se asume la inocencia de una persona (hipótesis nula), la condena a pesar de la inocencia sería un error del primer tipo. En cambio, si se dejara libre a la persona en cuestión y fuera culpable, se cometería un error del segundo tipo.
La probabilidad con la que puede evitarse ese segundo tipo de error, es decir, la aceptación errónea de la hipótesis nula, describe ahora el poder discriminatorio o poder estadístico de una prueba. Matemáticamente, esto puede expresarse en consecuencia como 1 – β, cuando β es la probabilidad de cometer un segundo tipo de error. Si β es pequeño, la potencia estadística es alta. Y viceversa.
Poder estadístico: ¿Qué entra?
Además del método estadístico utilizado, hay otros factores que determinan la potencia estadística. Por ejemplo, parece lógico que una gran diferencia entre dos poblaciones tenga menos probabilidades de pasar desapercibida que una pequeña (es más fácil detectar la diferencia de peso entre ratones y elefantes que entre ratones y ratas). Así, con una diferencia real creciente, el poder discriminatorio también aumenta. Lo mismo se aplica a una dispersión decreciente. Cuanto menor sea la dispersión de los datos, mejor podrán reconocerse las diferencias existentes. O bien: si hubiera ratones que pesaran 5 toneladas y elefantes que pesaran 20 gramos, la diferencia de peso sería probablemente menos fácil de demostrar. Un factor importante -e influenciable- en este ámbito es el tamaño de la muestra, ya que el error estándar se reduce al aumentar el tamaño de la muestra. Así, es más probable que los efectos más pequeños se separen con una muestra de mayor tamaño. El nivel de significación, es decir, la probabilidad de cometer un error del primer tipo, también influye en la potencia estadística.
En este marco, tiene sentido evaluar el poder discriminatorio de un diseño de estudio antes de aplicarlo. Porque en este punto, por ejemplo, el tamaño de la muestra aún puede ajustarse. Los análisis de potencia pueden utilizarse para decidir cuántos sujetos son necesarios para realizar un estudio de forma significativa. Un análisis de potencia realizado posteriormente -normalmente en ausencia de resultados significativos- puede proporcionar información sobre cuántos sujetos adicionales habrían sido necesarios, pero suele ser demasiado tarde. Normalmente se elige un poder discriminatorio en torno al 80%, por lo que la probabilidad de pasar por alto una diferencia significativa suele rondar el 20%. Una solución de compromiso clásica, después de todo, un aumento de la potencia estadística al 90% requeriría un aumento aproximado del 30% del tamaño de la muestra. La conclusión: Un resultado negativo de un estudio no se debe necesariamente a una falta de efecto. Quizá la muestra era demasiado pequeña, la dispersión demasiado grande, el efecto demasiado débil o la evaluación estadística mal elegida.
Literatura:
- StatistikGuru, Versión 1.96: Poder estadístico. https://statistikguru.de/lexikon/statistische-power.html (última consulta: 27.09.2021).
- Bortz J: Estadística – para científicos sociales. 5ª edición: Springer-Verlag Berlin Heidelberg; 1999.
InFo ONCOLOGÍA Y HEMATOLOGÍA 2021; 9(5): 25