En muchos estudios clínicos, el análisis de regresión es una base importante de la evaluación estadística y, por tanto, de los resultados encontrados. Por ejemplo, la mayoría de los médicos habrán oído hablar o leído sobre la regresión de Cox. Si las variables A y B tienen una relación lineal puede demostrarse matemáticamente desde el desarrollo de la regresión a finales del siglo XIX por Galton. Hasta el día de hoy, se ha hecho mucho para poder cartografiar incluso las interacciones complejas.
A menudo la pregunta de un ensayo clínico es clara: ¿Está x relacionado con y? O, por poner un ejemplo más concreto que se utiliza mucho en oncología: ¿Tiene la edad del paciente algún efecto sobre la supervivencia global? En este caso, la edad puede denominarse variable independiente y la supervivencia global, variable dependiente. Así que examinamos los efectos potenciales de la variable independiente sobre la variable dependiente. Hasta aquí, todo sencillo. La influencia de otros factores -otras variables independientes- es un factor de complicación adicional en cada caso. Así pues, no sólo la edad influye en el resultado, sino también, por ejemplo, la terapia, el sexo y quizá incluso la fase de la luna durante la administración de la medicación. Lo que nos lleva a un punto importante que nunca debe olvidarse en la interpretación de los análisis de regresión: ¡Como es bien sabido, una correlación no implica causalidad!
Idealmente, un análisis de regresión debería ser capaz de distinguir los distintos efectos de las diferentes variables independientes sobre la variable dependiente. Hoy en día existen multitud de métodos estadísticos para este fin, que se utilizan en función de la situación y de la pregunta. También es importante distinguir entre análisis de regresión y de varianza.
Diferentes formas de análisis de regresión
La elección del método de análisis más adecuado depende del número de variables a estudiar y del tipo de escala (Tabla 1) [2]. En principio, para realizar un análisis de regresión lineal, debe existir una relación lineal entre las variables. Una medida de la linealidad entre dos variables es el coeficiente de correlación de Pearson . Además, las variables independientes no deben estar correlacionadas entre sí y deben tener una distribución aproximadamente normal [2]. Otro requisito es la homocedasticidad: el valor del error de la variable independiente debe ser el mismo para cada valor. El resto lo hace el software estadístico, mediante el llamado “coeficiente de determinación”R2, que expresa lo bien que la ecuación de regresión refleja la relación entre las variables. La prueba F y, en el caso de varias variables independientes, la prueba t [3] determinan si la correlación hallada es estadísticamente significativa y, por tanto, si puede trasladarse de la muestra a la población.
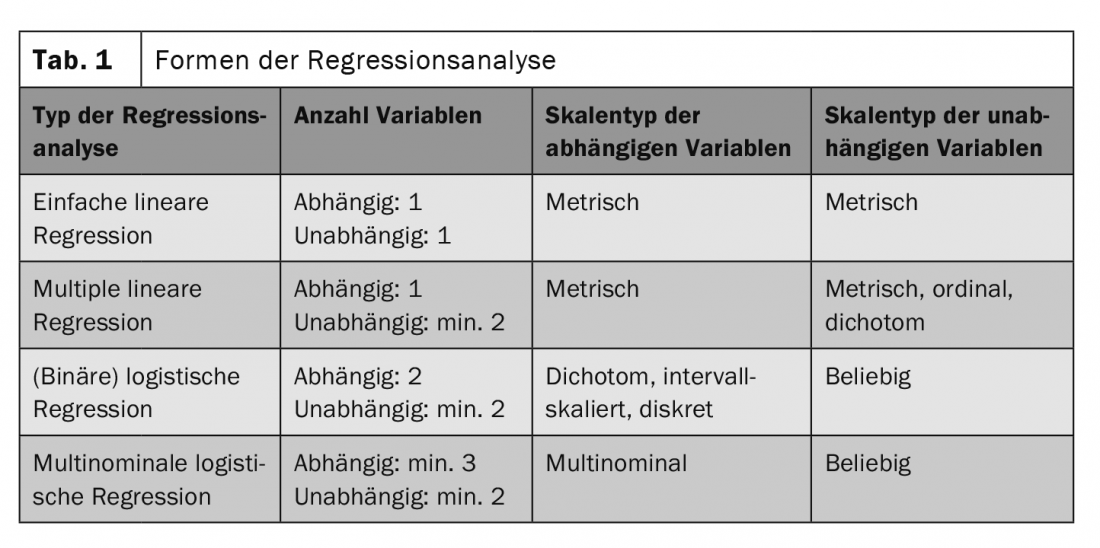
según [2]
¿Y cuál es la diferencia entre y el análisis de la varianza (ANOVA)?
Tanto el análisis de regresión como el análisis de varianza( ANOVA) son métodos estándar en diversos programas estadísticos, y sus ámbitos de aplicación se solapan. Mientras que el análisis de regresión se desarrolló originalmente para examinar variables métricas independientes como la edad, el análisis de la varianza en su origen sirvió principalmente para analizar variables independientes nominales como la elección del tratamiento. Ambos métodos de análisis pueden utilizarse hoy en día tanto con variables independientes métricas como nominales [4]. Así que la elección correcta no es tan fácil, sobre todo es una pregunta legítima y debe discutirse con un estadístico.
Literatura:
- Hemmerich W: StatistikGuru Versión 1.96: Regresión, análisis de regresión. https://statistikguru.de/lexikon/regression-regressionsanalyse.html (última consulta: 23.12.2021)
- Qualtrics: Análisis de regresión: procedimiento, objetivos y ejemplos. www.qualtrics.com/de/erlebnismanagement/marktforschung/regressionsanalyse (última consulta: 23.12.2021)
- Análisis de regresión – Definición de Statista https://de.statista.com/statistik/lexikon/definition/113/regressionsanalyse/ (último acceso 23.12.2021)
- Smigierski J: ¿Cuándo debe calcularse un análisis de varianza y cuándo un análisis de regresión? www.beratung-statistik.de/statistik-infos/statistik-beratung-faqs/unterschied-varianzanalyse-regressionsanalyse (última consulta: 23.12.2021)
PRÁCTICA DERMATOLÓGICA 2022; 32(1): 48
InFo ONCOLOGÍA Y HEMATOLOGÍA 2022; 10(1): 41