La cardiopatía isquémica es el resultado de un flujo sanguíneo coronario inadecuado. La medición directa del flujo sanguíneo absoluto (ml/min) es posible, pero no se ha introducido en la rutina clínica de la mayoría de los laboratorios de cateterismo. Recientemente se ha descrito un método de dinámica de fluidos computacional ( CFD) para predecir el flujo que distingue entre flujo de entrada, de rama lateral y de salida durante la angiografía. Un estudio reciente ha evaluado ahora un nuevo método que regionaliza el flujo a lo largo de la arteria.
La cardiopatía isquémica (CI) es la principal causa de muerte en todo el mundo y es el resultado de una insuficiencia del flujo sanguíneo coronario (Q), generalmente causada por una enfermedad oclusiva coronaria. Incluye una variedad de síndromes clínicos como la isquemia sintomática (angina de pecho), el infarto de miocardio y la insuficiencia cardiaca. Los tratamientos intervencionistas son eficaces para restablecer el Q, pero sólo deben dirigirse a las lesiones que provocan isquemia. Sin embargo, para el uso clínico rutinario en el laboratorio de cateterismo cardiaco, no se dispone de ninguna técnica para medir el Q directamente. Durante varias décadas, los cardiólogos han confiado en marcadores indirectos sustitutivos, como el tiempo de tránsito medio derivado de la termodilución, la velocidad de flujo derivada del Doppler y la reserva fraccional de flujo (RFF) derivada de la presión [2-4] y, más recientemente, la RFF “virtual” derivada de la imagen angiográfica (RFFv) [5]. Todos estos métodos tienen puntos fuertes y débiles, pero ninguno mide el Q “absoluto” en mL/min.
Se han desarrollado dos métodos para cuantificar el Q: El primero, la termodilución en infusión continua (CIT), es el método más establecido y validado y utiliza el catéter de infusión Rayflow™ [6,7]. El segundo, virtuQ™, obtiene Q a partir de una simulación CFD basada en la anatomía de la angiografía 3D y en las mediciones del cable de presión. Ambos métodos cuantifican también la resistencia microvascular absoluta (Rmicro), proporcionando una evaluación exhaustiva de toda la circulación coronaria. Una limitación del método CFD era que sólo se tenía en cuenta el vaso principal y no se consideraba el flujo en las ramas laterales [8]. Esto puede ser aceptable para el cálculo de vFFR, que sólo interroga los efectos de una lesión localizada, pero no para el cálculo de Q, que depende de la lesión, las ramas laterales y la estructura de los microvasos [9].
Un estudio reciente describió un método de simulación de pared porosa que utiliza leyes de escala morfométrica establecidas y conocimientos específicos de cada caso sobre la conicidad arterial para permitir que la sangre salga del vaso principal en proporción al flujo de las ramas laterales [9]. Una limitación de este enfoque era que el flujo de las ramas laterales se distribuía difusamente a lo largo de toda la longitud del vaso principal. Por lo tanto, este enfoque no captó los efectos hemodinámicos de un gran volumen de pérdida de flujo regionalizada en las grandes ramas laterales arteriales. Un estudio reciente describe un método novedoso que intenta correlacionar las “fugas” en las ramas laterales con las zonas de bifurcaciones significativas y, por tanto, representa el patrón de flujo que suele encontrarse en las arterias coronarias reales. El objetivo era validar este nuevo método mediante mediciones CIT y comparar los resultados con los del método CFD homogéneo [1].
Recogida de datos clínicos
La FFR se midió en las arterias de interés utilizando tecnología estándar (PressureWire™) y una deriva de señal máxima tolerada de 2 mmHg [10], el catéter de infusión Rayflow™ y el sistema Coroventis™ [6,7] se utilizaron para cuantificar Q (QCIT) y Rmicro (RmicroCIT). Las mediciones de termodilución se realizaron en la arteria coronaria proximal, mientras que las mediciones de presión bajo hiperemia inducida por sal se realizaron 6 cm distal a la punta del catéter de infusión [7].
Simulación del flujo sanguíneo coronario
Para reconstruir la anatomía coronaria se utilizaron dos proyecciones angiográficas del vaso de interés, tomadas con ≥30° de separación y durante la diástole final. La selección de imágenes y la corrección del movimiento de la mesa entre pases de angiografía se realizaron manualmente, mientras que el seguimiento de la línea central y la detección de los bordes de los vasos se realizaron de forma semiautomática utilizando el gradiente de contraste para ambas imágenes, con la corrección manual necesaria. Por último, se creó automáticamente una geometría 3D rígida y axisimétrica que representaba la anatomía del paciente. La entrada de las arterias reconstruidas correspondía a la ubicación de la medición invasiva de QCIT y Pa, mientras que la salida correspondía a la ubicación de la Pd. Las mediciones de la presión invasiva se utilizaron para definir las condiciones límite de entrada y salida. La simulación CFD se realizó utilizando parámetros sanguíneos estándar (densidad 1056 kg/m3; viscosidad 0,0035 Pa s), que modelan un flujo laminar y constante de un fluido newtoniano [11,12].
Simulación del flujo del ramal lateral
En el estudio actual, el flujo en las ramas laterales se simuló modelando reconstrucciones arteriales con un límite de pared porosa. Esto permitió una pérdida de flujo del lumen del vaso principal. El tamaño de las ramas laterales se derivó de la conicidad del vaso principal utilizando la ley de Murray [13] que relaciona los diámetros (D) del vaso principal (PV) y de las ramas laterales (DB) alrededor de una rama:
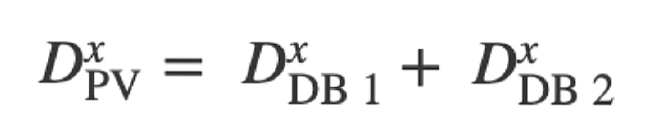
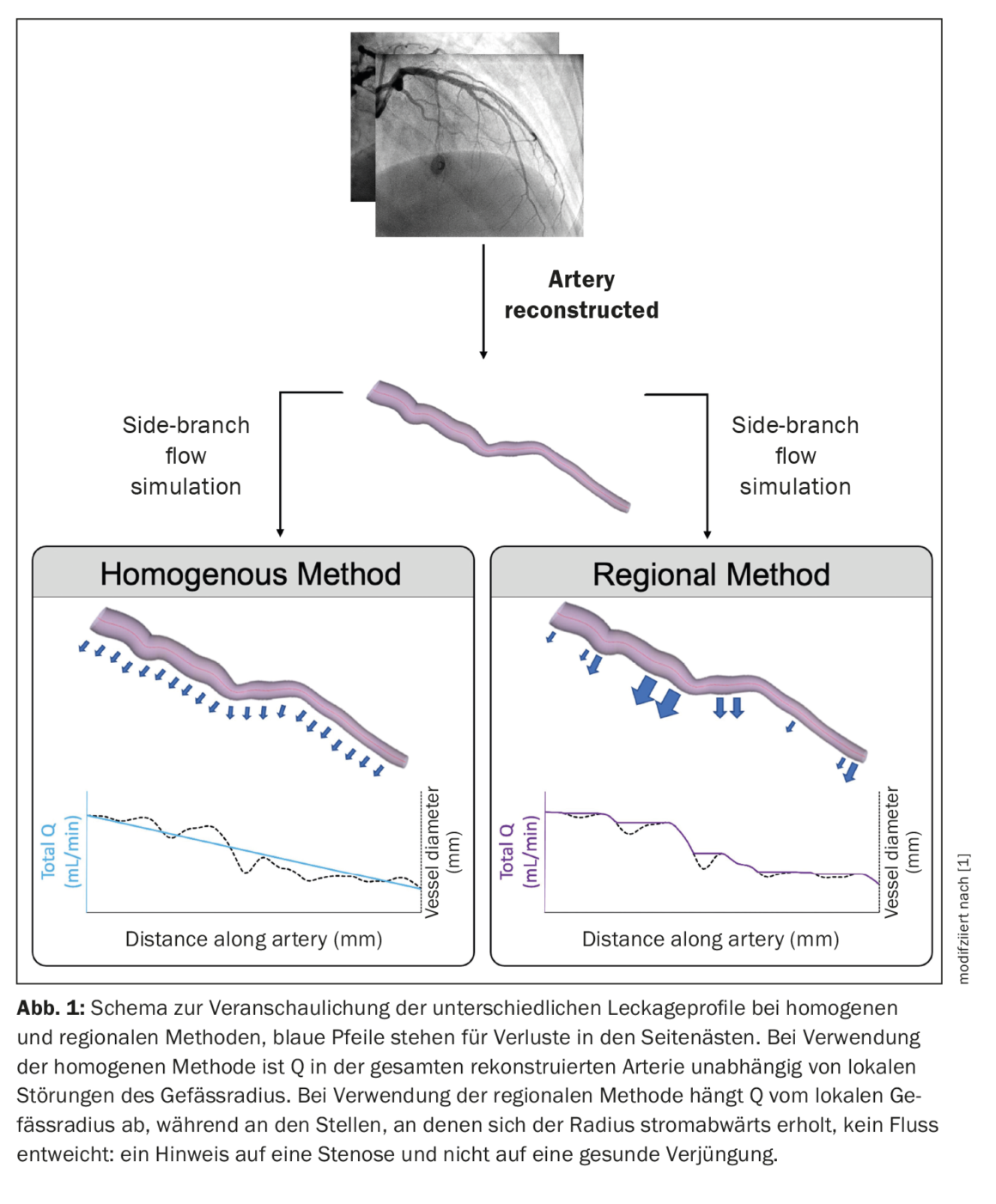
donde “x” representa una constante cuyo valor varía entre 2,0 y 3,0 [14–16]. El alcance del flujo del ramal lateral dependía del valor utilizado para esta constante de proporcionalidad y del método empleado para distribuir las pérdidas del ramal lateral (homogéneo frente a regional). El objetivo era comparar la precisión de los métodos homogéneo y regional con las masas derivadas de forma invasiva. El método de la pared porosa homogénea distribuyó las pérdidas de la rama lateral uniformemente a lo largo de toda la longitud del vaso reconstruido y no se vio afectado por el ahusamiento local. En el método de la pared porosa regional, las pérdidas de flujo de las ramas laterales se distribuyeron proporcionalmente al estrechamiento local del vaso sano. Esto se hizo para regionalizar mejor la Q. En los vasos sanos, el rejuvenecimiento regional se produce en los puntos de ramificación. Por lo tanto, este método debería regionalizar con mayor precisión el flujo sanguíneo en la arteria in vivo. Para distinguir el rejuvenecimiento de los vasos sanos de la reducción del diámetro causada por las placas ateroscleróticas, se utilizó un filtro de detección de estenosis que excluía las fugas de la pared porosa en las secciones con recuperación descendente del diámetro del vaso (Fig. 1) [1].
Casos clínicos
De los 48 casos originales, 27 casos de 20 pacientes proporcionaron conjuntos completos de datos fisiológicos. Siete pacientes (35%) eran varones, la edad media era de 62 (±10) años y el índice de masa corporal (IMC) medio era de 25,2 (±3,6) kg/m2. Los 27 casos afectaron a la arteria descendente anterior izquierda (DAI) (n=18), la arteria circunfleja izquierda (Cx) (n=7) y la arteria coronaria derecha (ACD) (n=2). El QCIT medio fue de 219 (±61) mL/min y el RmicroCIT medio fue de 360 [290–450] mmHg min/L. La mayoría de los casos incluidos presentaban una enfermedad epicárdica mínima, con una FFR media de 0,87 (±0,08) y sólo tres casos alcanzaron el umbral clínico de significación de la FFR (≤0,80). La mediana del porcentaje de estenosis determinada por el cirujano, la QCA 2D y la QCA 3D fue del 10% [0–25%], el 16% [0–31%] y el 15% [0–33%], respectivamente. Ninguno de los casos incluidos presentaba enfermedad epicárdica difusa. Utilizando un umbral de 460 mmHg min/L25-27, cinco (25%) pacientes tenían una MVD clínicamente significativa evaluada mediante RmicroCIT.
El método de la pared porosa homogénea
El método de limitación de pared porosa homogénea dio un QCFD medio de 219 (±86) mL/min. Hubo una correlación estadísticamente significativa entre QCFD y QCIT (r=0,473, p=0,006), la regresión de paso y Bablok identificó diferencias constantes y proporcionales entre las técnicas (coeficiente c -202, IC 95% -633 a -20; coeficiente m 2,03, IC 95% 1,15 a 4,07), el delta medio entre las técnicas fue cero y los límites de concordancia Bland-Altman al 95% fueron de -168 a +168 ml/min. Las diferencias proporcionales entre QCFD y QCIT se caracterizaron por un aumento del sesgo a caudales más elevados, representado visualmente por el análisis de Bland-Altman. También se observó una correlación significativa entre la RmicroCFD y la RmicroCIT (r=0,647, p=0,0001), hubo diferencias constantes y proporcionales (coeficiente c -400, IC 95% -950 a -90; coeficiente m 2,07, IC 95% 1,15 a 3,67), el delta medio entre técnicas fue de +30 mmHg min/L y los límites de concordancia Bland-Altman al 95% fueron de -210 a +480 mmHg min/L.
El método del límite regional de la pared porosa
El método del límite regional de la pared porosa dio un QCFD medio de 219 (±96) mL/min. La correlación entre QCFD y QCIT fue significativa (r=0,429, p=0,0127), la regresión de paso y Bablok identificó diferencias constantes y proporcionales entre las técnicas (coeficiente c -220, IC del 95%: -687 a -16; coeficiente m 2,12, IC del 95%: 1,18 a 4,19), el delta medio entre las técnicas fue cero y los límites de concordancia de Bland-Altman al 95% fueron de -175 a +175 ml/min. La concordancia entre la QCFD y la QCIT no fue mejor ni para las técnicas homogéneas ni para las regionales (t=0,0023, p=0,998). También se observó una correlación significativa entre la RmicroCFD y la RmicroCIT (r=0,586, p=0,0006), hubo diferencias constantes y proporcionales (coeficiente c -400, IC 95% -1030 a -60; coeficiente m 2,09, IC 95% 1,04 a 3,90), el delta medio entre técnicas fue de +37 mmHg min/L y los límites de concordancia Bland-Altman al 95% fueron de -220 a +540 mmHg min/L. La concordancia entre RmicroCFD y RmicroCIT no fue mejor ni para el método homogéneo ni para el regional (U=363, p=0,944). Con un umbral de 460 mmHg min/L, siete (35%) pacientes presentaban una MVD clínicamente significativa evaluada mediante RmicroCFD. Utilizando la RmicroCIT como medición de referencia, la sensibilidad, la especificidad, el valor predictivo positivo y el valor predictivo negativo de la técnica CFD fueron del 80%, 80%, 57% y 92%, respectivamente.
Determinantes del cumplimiento
Ciertas características de los pacientes y los vasos parecían influir en la concordancia entre la DFC y las mediciones invasivas. Para los métodos de límites de pared porosa homogénea resp. métodos de frontera de pared porosa regional, la concordancia Q se correlacionó significativamente con la caída de presión transversal (Pa-Pd) (r=0,449, p=0,0094; r=0,391, p=0,0217), FFR (r=-0,399, p=0,0196; r= -0,334, p=0,0441) y el porcentaje de estenosis evaluado mediante QCA 2D (r=0,355, p=0,0345; r=0,472, p=0,0065) y 3D (r=0,369, p=0,0292; r=0,489, p=0,0048). Esto significó que, tanto para el método homogéneo como para el regional, la concordancia entre el QCFD y el QCIT mejoró para los casos con mayor carga de enfermedad identificados por los estudios con cables de presión, el QCA 2D y el QCA 3D. Para el método regional, la concordancia Q también se correlacionó con la estenosis evaluada visualmente (r=0,371, p=0,0282).
Para el método Rmicro, tanto el método homogéneo como el regional se correlacionaron con la caída de presión transversal (r=0,359, p=0,0330; r=0,340, p=0,0415, respectivamente) y la FFR (r=-0,368, p=0,0295; r=-0,364, p=0,0310, respectivamente), pero no se observó ningún efecto para la evaluación de la estenosis. Esto significó, tanto para la técnica homogénea como para la regional, que la concordancia entre la RmicroCFD y la RmicroCIT mejoró en los casos con mayor carga de enfermedad evaluada mediante la prueba de cables de presión, mientras que la carga de enfermedad evaluada mediante el porcentaje de estenosis no se asoció con la concordancia.
Variabilidad intraoperador
Para los métodos de confinamiento homogéneo y de pared porosa regional, la variabilidad QCFD fue del 7,8% (±4,2%) y del 5,6% (±2,7%), respectivamente. Para RmicroCFD fue del 2,6% [4,6–6,1%] y del 3,2% [1,9–10,2%] respectivamente. La variabilidad intraobservador no difirió entre las técnicas homogéneas y las regionales ni para la QCFD (U=33, p=0,218) ni para la RmicroCFD (U=45, p=0,739).
Flujo coronario en la entrada, salida y ramas laterales regionalizable
En el estudio retrospectivo, se validó un método de límites de pared porosa regionalizado para simular el Q lateral y se compararon los resultados con los del método homogéneo original [15]. El objetivo principal era regionalizar el flujo del brazo lateral y del brazo principal. Esto se consiguió sin cambiar significativamente el flujo global en el brazo lateral en comparación con el método homogéneo. El nuevo método regionalizado se correlacionó con las mediciones del CIT con una desviación de cero y un límite de concordancia del 95% de ±175 mL/min. La concordancia con las mediciones clínicas invasivas fue subóptima, lo que puede deberse a la inclusión de múltiples casos de INOCA con estenosis y gradiente de presión mínimos.
Durante la angiografía y la evaluación con guía de presión, el flujo coronario puede ahora regionalizarse y diferenciarse en la entrada, la salida y las ramas laterales. El efecto de la enfermedad epicárdica sobre la concordancia sugiere que el modelo se adapta mejor a los casos con estenosis cerca de las ramas laterales.
Literatura:
- Taylor DJ MA, et al.: Validation of a novel numerical model to predict regionalized blood flow in the coronary arteries. EurHeartJ 2023.
https://doi.org/10.1093/ehjdh/ztac077 - Gould KL, Lipscomb K, Hamilton GW: Physiologic basis for assessing critical coronary stenosis. Instantaneous flow response and regional distribution during coronary hyperemia as measures of coronary flow reserve. Am J Cardiol 1974;33: 87–94.
- De Bruyne B, Paulus WJ, Vantrimpont PJ, et al.: Transstenotic coronary pressure gradient measurement in humans: in vitro and in vivo evaluation of a new pressure monitoring angioplasty guide wire. J Am Coll Cardiol 1993;22: 119–126.
- Fearon WF, Balsam LB, Farouque HM, et al.: Novel index for invasively assessing the coronary microcirculation. Circulation 2003;107: 3129–3132.
- Ghobrial M, Haley HA, Gosling R, et al.: The new role of diagnostic angiography in coronary physiological assessment. Heart 2021;107: 783–789.
- Aarnoudse W, Van’t Veer M, Pijls NH, et al.: Direct volumetric blood flow measurement in coronary arteries by thermodilution. J Am Coll Cardiol 2007;50: 2294–2304.
- van’t Veer M, Adjedj J, Wijnbergen I, et al.: Novel monorail infusion catheter for volumetric coronary blood flow measurement in humans: in vitro validation. EuroIntervention 2016;12: 701–707.
- Morris PD, Gosling R, Zwierzak I, et al.: A novel method for measuring absolute coronary blood flow & microvascular resistance in patients with ischaemic heart disease. Cardiovasc Res 2020;117: 1567–1577.
- Gosling RC, Sturdy J, Morris PD, et al.: Effect of side branch flow upon physiological indices in coronary artery disease. J Biomech 2020;103: 109698.
- Pijls NH, van Son JA, Kirkeeide RL, et al.: Experimental basis of determining maximum coronary, myocardial, and collateral blood flow by pressure measurements for assessing functional stenosis severity before and after percutaneous transluminal coronary angioplasty. Circulation 1993;87: 1354–1367.
- Morris PD: Computational fluid dynamics modelling of coronary artery disease. PhD thesis. University of Sheffield 2015. https://etheses.whiterose.ac.uk/11772/1/CFD Modelling of CAD Morris_
submitted.pdf - Brown AG, Shi Y, Marzo A, et al.: Accuracy vs. computational time: translating aortic simulations to the clinic. J Biomech 2012;45: 516–523.
- Murray CD: The physiological principle of minimum work: I. The vascular system and the cost of blood volume. Proc Natl Acad Sci USA 1926;12: 207.
- Huo Y, Kassab GS: Intraspecific scaling laws of vascular trees. J R Soc Interface 2012;9: 190–200.
- Kamiya A, Togawa T: Optimal branching structure of the vascular tree. Bull Math Biophys 1972;34: 431–438.
- Murray CD: The physiological principle of minimum work: I. The vascular system and the cost of blood volume. Proc Natl Acad Sci U S A 1926;12: 207–214.
CARDIOVASC 2023; 22(1): 32–34