In many clinical studies, regression analysis is an important basis of statistical evaluation – and thus of the results found. For example, most physicians have probably also heard or read about Cox regression. Whether variables A and B have a linear relationship can be proven mathematically since the development of regression at the end of the 19th century by Galton. Up to the present day, a lot has been done to be able to map even complex interactions.
Often the question of a clinical trial is clear: Is x related to y? Or, to take a more concrete example widely used in oncology: Does patient age have an impact on overall survival? In this case, age can be referred to as the independent variable, and overall survival as the dependent variable. Thus, we examine potential effects of the independent variable on the dependent variable. So far, so simple. The influence of other factors – other independent variables – is an additional complicating factor in each case. Thus, not only does age influence outcome, but also, for example, therapy, gender, and perhaps even the phase of the moon during medication administration. This brings us to an important point that should never be forgotten in the interpretation of regression analyses: As is well known, a correlation does not imply causality!
Ideally, a regression analysis should be able to tease apart the different effects of different independent variables on the dependent variable. Today, a variety of statistical methods exist for this purpose, which are used depending on the situation and the question at hand. It is also important to distinguish between regression and variance analysis.
Different forms of regression analysis
The choice of the most appropriate method of analysis depends on the number of variables to be studied and the type of scale (Table 1) [2]. In principle, for a linear regression analysis, there must be a linear relationship between the variables. A measure for the linearity between two variables is the Pearson correlation coefficient . In addition, the independent variables should be uncorrelated and approximately normally distributed [2]. Another requirement is homoscedasticity: the error value of the independent variable should be the same for each value. The rest is then done by the statistical software, where the so-called “coefficient of determination”R2 expresses how well the regression equation reflects the relationship between the variables. Whether the correlation found is statistically significant – and thus may be transferred from the sample to the population – is determined by the F-test and, in the case of several independent variables, the t-test [3].
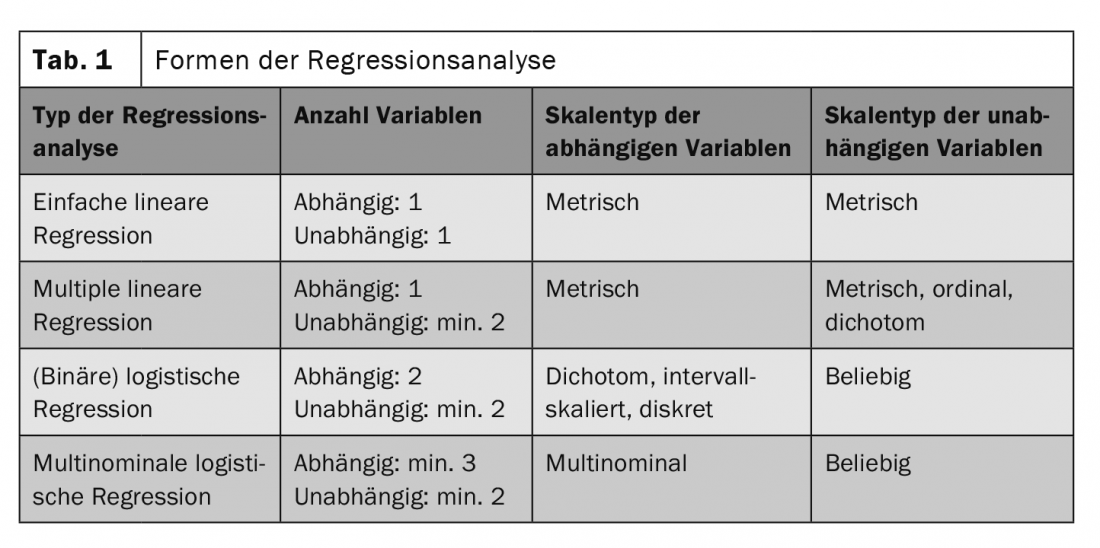
according to [2]
And what is the difference to analysis of variance (ANOVA)?
Regression analysis and analysis of variance( ANOVA) are both standard methods in various statistical programs, and the areas of application overlap. While regression analysis was originally developed to examine independent metric variables such as age, analysis of variance in its origin served primarily to analyze nominal independent variables such as treatment choice. Both analysis methods can be used today with both metric and nominal independent variables [4]. So the right choice is not so easy, mostly a legitimate question and should be discussed with a statistician.
Literature:
- Hemmerich W: StatistikGuru Version 1.96: Regression, Regression Analysis. https://statistikguru.de/lexikon/regression-regressionsanalyse.html (last accessed 23.12.2021)
- Qualtrics: Regression analysis: process, objectives & examples. www.qualtrics.com/de/erlebnismanagement/marktforschung/regressionsanalyse (last accessed 23.12.2021)
- Regression analysis – Statista definition https://de.statista.com/statistik/lexikon/definition/113/regressionsanalyse/ (last accessed 12/23/2021).
- Smigierski J: When to calculate an analysis of variance and when a regression analysis? www.beratung-statistik.de/statistik-infos/statistik-beratung-faqs/unterschied-varianzanalyse-regressionsanalyse (last accessed 23.12.2021)
DERMATOLOGIE PRAXIS 2022; 32(1): 48
InFo ONCOLOGY & HEMATOLOGY 2022; 10(1): 41.